| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 경기도 버스
- C# MDB Handle
- DrawRectangle
- Winform
- C# 파일 암/복호화
- TDD
- Excel Cell Format
- 객체지향
- 시
- 공공 데이터 포털
- Json.NET
- C# MDB
- WPF
- GDI+
- 버스 API
- eventhandler
- JSON
- sqlite3
- 디자인 패턴
- c#
- 경기도 버스정보시스템
- MVC
- MDB Select
- delegate
- NUnit
- solid
- Cell Border Style
- MDB Connect
- DrawEllipse
- eventargs
- Today
- Total
목록IT Engineering/Data Mining (8)
White Whale Studio
 K-medoids Clustering Algorithm
K-medoids Clustering Algorithm
해당 포스팅은 위키피디아 의 내용을 본인이 이해하기 쉽게 풀어쓴 내용을 담고 있습니다. 부정확한 정보가 포함 될 수 있으며, 좀더 정확한 정보를 확인하고자 하시는 분은 위키피디아 및 다른 사이트를 참조해주시기 바랍니다. K-medoids 클러스터링 알고리즘은 K-means와 흡사하다. 다만 K-means가 임의의 좌표를 중심점으로 잡는 반면 K-medoids는 실제 점 하나를 중심점으로 잡아서 계산을 수행한다. 약간의 계산상의 차이가 있지만 대체적으로 유사한 부분이 많다. K-medoids의 대표적인 방법은 Partitioning Around Medoids(PAM) 알고리즘인데 이에 대해서 살펴보도록하자. 전체적인 단계는 다음과 같다. K-medoids의 단계 1. 초기화 : n개의 데이터 포인트에서 임..
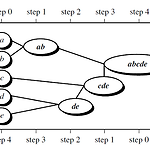 계보적 방법(Hierarchical Clustering)
계보적 방법(Hierarchical Clustering)
앞에서 군집화 기법에 대해 정리를 할때 언급했었던 계보적 방법이다. 개념적인 부분은 앞의 부분과도 겹치지만 다시한번 살펴보자. 확실히 영어가 더 인식하기에 편하다. Hierarchical Clustering 계보적 군집화는 병합적 방법과 분할적 방법으로 나뉜다. ㆍ병합적 계보적 군집화(Agglomerative) : 상향식 방법, 각 객체를 자신의 군집에 배치하고, 그 원자 군집들을 더 큰 군집으로 만들어 간다. 모든 객체가 하나의 군집이 되거나, 종료조건을 만족하면 종료, 대부분의 군집화 방법(유사성에 대한 정의만 다름) ㆍ분할적 계보적 군집화(Divisive) : 병합적 방법과 반대, 하향식, 모든 객체를 하나의 군집으로 여기면서 시작, 각 객체가 하나의 군집을 형성하게 될때까지, 혹은 적절한 개수의 ..
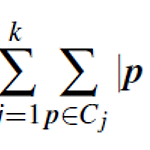 k-medoids(중앙객체) 방법과 CLARANS
k-medoids(중앙객체) 방법과 CLARANS
이것은 각막셀카! 아... 군집분석도 타이핑하려니 귀찮다.. 앞으로 생략.. ---------------------------------------------------- 앞에서 포스팅했듯이 k-means는 평균값을 구하는 연산을 수행하기 때문에 잡음이나 이상치에 민감하다고 했다. 이러한 단점을 해결하기 위해서 나온것이 k-medoids 알고리즘이다. K-medoids 알고리즘의 핵심은 평균을 구하는 대신에 군집을 대표하는 실제 객체를 선택하는 것이다. 나머지 객체들은 가장 유사한 대표 객체들로 군집화 된다. 즉, K-means에서 평균을 계산해서 평균값을 기준으로하여 가장 가까운 객체들은 특정 군집에 할당을 했다면, K-medoids는 실제로 존재하는 객체들 중에 하나를 선택하여 대표 객체로 선정하고 ..
n 개의 객체를 가진 데이터 집합 D와 군집 수로 k가 주어진다면, 분할 알고리즘은 객체들을 나누어 k개의 군집으로 나눈다. 결과적으로 군집 내의 객체들은 유사하고, 다른 군집의 객체들끼리는 그렇지 않도록하는 것이 최종목적이 되겠다. 가장 잘 알려진 일반적인 분할 방법은 k-means와 k-mediods 이다. k-평균, k-중앙객체 라고도 한다. 먼저 k-means에 대해 살펴보자. k-means는 개괄적으로 표현하자면, 간단하지만 단점이 좀 있는 클러스터링 방법이다. 그도 그럴것이 초기값으로 k가 주어져야만 하고, 초기 설정값에 따라서 클러스터링 결과가 많이 바뀌기 때문에 여러가지 방면에서 약점이 있다. 상세하게 조금씩 살펴보자. 진행 순서는 다음과 같다. 1. 군집의 평균이나 중심값으로 객체들에서 ..
생각보다 많은 클러스터링 기법... 하나씩 찬찬히 살펴보자. 1. 분할 기법(Partitioning methods) : 대표적인 예로는 K-mean, K-medoid 기법이 있다. K-mean 기법이야 워낙 유명하니까 대충 감이 잡힐것 같다. 상세히 살펴보자. n 개의 객체 혹은 튜플이 주어졌을 때, 분할 기법은 의 조건을 만족하도록 군집을 나타내틑 데이터 분할을 k개 만든다. 즉 12개의 튜플이 있다고 할때 이 튜플들을 3개씩 묶게 되면 총 4개의 군집이 생성된다. 이 경우 n = 12, k = 4가 되는 것이다. 분할 기법에는 2가지 조건이 있다. 1) 각 그룹은 적어도 하나의 객체를 가지고 있어야 한다. 2) 각 객체는 정확히 하나의 그룹에 속해야 한다. 위의 조건에 근거하여 분할 기법은 분할의 수..
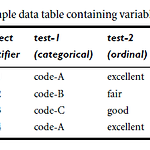 군집분석[Cluster Analysis] - 3 범주형, 순서형, 비율척도 변수
군집분석[Cluster Analysis] - 3 범주형, 순서형, 비율척도 변수
범주형 변수 (Categorical Variables) 둘이 상의 상태를 가질 수 있는 이항형 변수의 일반적인 형태이다. 예를 들면 무지개 색깔은 빨주노초파남보 인것처럼말이다. 범주형 변수의 상이성은 어떻게 계산할까? 두 객체 i와 j간의 상이성은 불일치의 비율을 이용하여 계산한다. p는 변수의 총 개수 이고, m은 객체 i와 j가 같은 상태인 변수의 수, 즉 일치한 수를 뜻한다. 표 7.3을 예로 한 번 보자. 객체 번호에 따라서 서로 다른 속성 test 1, 2, 3이 다른 변수를 가진 상태이다. 우선 객체번호와 test-1 속성만 사용한다. 표에도 적혀져 있지않은가. 대충 유추해보면 범주형 변수의 변수는 code-A, code-B, code-C 일 것이다. 상이성 행렬을 계산하면 다음과 같다. 여기..
 군집분석[Cluster Analysis] - 2 이항형 변수[12.4.27]
군집분석[Cluster Analysis] - 2 이항형 변수[12.4.27]
◎ 이항형 변수 이항형 변수라니까 웬지 또 어렵다. 그러나 영어로는 Binary Variable 이라고 하면 쉽지? 0과 1 상태만을 가지는 변수다. 0은 변수가 존재하지 않는다는 것을 의미하고, 1은 존재한다는 것을 의미한다. 예로 0일때는 안경 낀 아이, 1일 때는 안경 안낀 아이로 판단할수 있다는 거다. 대칭이거나 비대칭인 이항형 변수로 표현된 객체간의 상이성을 계산하는 방법을 설명한다. 대칭과 비대칭은 차이는 또 무엇인가? 대칭은 각 상태가 모두 동등한 가치가 있고 같은 가중치를 가질때를 말한다. 즉, 결과가 0이나 1 어느 쪽으로 표시되어도 상관없다. 예를 들면 남자와 여자를 상태로 하는 gender 속성정도랄까.. 표 7.1을 보자. 모든 이항형 변수들이 같은 가중치를 가진것으로 여겨진다면 표..
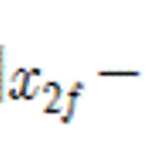 군집분석[Cluster Analysis] - 1 개념 및 데이터 유형
군집분석[Cluster Analysis] - 1 개념 및 데이터 유형
군집분석[Cluster Analysis] 군집이라고 하면, 모임, 집단과 같은 의미로 보면된다. 책자에 나온 내용이나 사전적인 의미로 정리하자면 물리적 혹은 추상적 객체들을 비슷한 객체로 그룹화하는 것을 군집화(Clustering)이라고 한다. 데이터마이닝 기법 중 하나인 군집 분석은 이미 많은 연구가 이루어져 왔고, 다양한 응용을 위한 연구 또한 진행되고 있다. 군집 분석 자체가 인간과 밀접한 관계를 가진다. 어릴 때부터, 사람은 지속적으로 무의식적으로 군집화를 시도함으로써 동식물을 구분하거나, 가족 친지 중에서도 나에게 편한사람, 좋은사람, 그리고 어려운 사람, 나쁜 사람과 같이 분류하는 방법을 배운다. 실제적으로 군집 분석이 응용되는 사례를 살펴보면, 패턴 인식, 데이터 분석, 이미지 처리, 시장조..
